本文目录一览：
- 1 、自适应滤波器的原理
- 2 、如何评价自适应滤波算法的优劣
- 3、自适应滤波器原理内容简介
- 4、自适应陷波滤波后信号变大
- 5 、自适应滤波方法——LMS算法
自适应滤波器的原理
自适应滤波器的原理 如图1所示。 图中x（j）表示 j 时刻的输入信号值 ，y（j）表示 j 时刻的输出信号值 ，d（j）表示 j 的参考信号值或所期望响应信号值，误差信号e（j）为d（j）与y（j）之差 。
自适应滤波器是一种基于输入和输出信号统计特性估计的算法或装置，通过自动调整滤波器系数 ，以实现最佳滤波效果 。这种滤波器可以分为连续域和离散域两种形式 ，其中离散域的自适应滤波器由抽头延迟线 、可变加权系数和自动调整系数的结构组成，如图所示 ，用于模拟未知离散系统的信号流程。
通常 ，自适应滤波器的核心是其系数，这些系数并非预设常数 ，而是由自适应算法实时更新的时变系数。这种特性使得自适应滤波器具有独特的适应性 ，能够自动地随着输入信号的变化，不断优化自身的响应 ，以达到理想的效果 。
你仔细看看自适应滤波器是能够根据输入信号自动调整性能进行数字信号处理的数字滤波器 。作为对比 ，非自适应滤波器有静态的滤波器系数，这些静态系数一起组成传递函数。对于一些应用来说 ，由于事先并不知道所需要进行操作的参数 ，例如一些噪声信号的特性，所以要求使用自适应的系数进行处理 。
如何评价自适应滤波算法的优劣
1、寻求收敛速度快 、稳态误差低 、计算复杂度低、跟踪能力强评价自适应滤波算法的优劣 。自适应滤波算法作为自适应滤波器的重要组成部分，直接决定着滤波性能的优劣。自适应滤波是近年以来发展起来的一种最佳滤波方法 。它是在维纳滤波 ，Kalman滤波等线性滤波基础上发展起来的一种最佳滤波方法 。
2 、通常 ，自适应滤波器的核心是其系数，这些系数并非预设常数 ，而是由自适应算法实时更新的时变系数。这种特性使得自适应滤波器具有独特的适应性 ，能够自动地随着输入信号的变化，不断优化自身的响应 ，以达到理想的效果 。
3 、非自适应滤波器则具有固定系数 ，这些系数决定了滤波器的性能，适用于信号统计特性已知的稳定环境 。然而 ，对于未知或动态变化的信号环境 ，自适应滤波器能够自动调整参数以优化滤波效果。自适应滤波器通过学习和估计信号的统计特性来调整系数，从而在不同信号条件下保持高性能 。
4、在时变问题中 ，自适应滤波算法的应用广泛 。然而 ，环境的非平稳性意味着最佳解可能随时间变化，甚至在某一时刻不是最佳解。随机梯度下降法在这种情境下提供了动态调整权重，以适应环境变化的能力。最小均方LMS算法是自适应滤波领域的一大亮点 ，由Widrow和Hoff于1960年提出 。
5 、自适应滤波算法广泛应用于系统辨识 、回波消除、自适应谱线增强 、自适应信道均衡 、语音线性预测、自适应天线阵等诸多领域中 。总之 ，寻求收敛速度快，计算复杂性低 ，数值稳定性好的自适应滤波算法是研究人员不断努力追求的目标。
自适应滤波器原理内容简介
1、自适应滤波器的原理 如图1所示 。 图中x（j）表示 j 时刻的输入信号值 ，y（j）表示 j 时刻的输出信号值，d（j）表示 j 的参考信号值或所期望响应信号值 ，误差信号e（j）为d（j）与y（j）之差 。
2 、自适应LMS横向滤波器 ，其原理与应用在章节中得到了深入剖析。自适应格型滤波器，这一技术在信号处理中的独特性能和应用场景也在书中有所阐述 。自适应递归滤波器 ，其动态调整能力在通信与信息系统中的重要性不容忽视 。
3 、) 逆模型：在这类应用中 ，自适应滤波器的作用是提供一个逆模型，该模型可在某种意义上最好拟合未知噪声装置。理想地 ，在线性系统的情况下 ，该逆模型具有等于未知装置转移函数倒数的转移函数，使得二者的组合构成一个理想的传输媒介 。该系统输入的延迟构成自适应滤波器的期望响应 。
4、自适应滤波器可以是连续域的或是离散域的。离散域自适应滤波器由一组抽头延迟线 、可变加权系数和自动调整系数的机构组成 。附图表示一个离散域自适应滤波器用于模拟未知离散系统的信号流图 。
5 、本文简明介绍自适应滤波理论，以统一形式囊括多种算法 ，避免冗余与繁杂表示。揭示自适应滤波坚实理论基础 ，重点探讨有限精度实现中真正有效的算法。第二版在原基础上新增非线性自适应滤波、子带自适应滤波 、线性约束维纳滤波器 、LMS算法快速自适应实现行为分析及仿射投影算法等全新内容与研究成果 。
6、自适应滤波原理：自适应滤波器由参数可调的数字滤波器（或称为自适应处理器）和自适应算法两部分组成，如图3-12所示 。参数可调数字滤波器可以是FIR数字滤波器或IIR数字滤波器 ，也可以是格型数字滤波器。
自适应陷波滤波后信号变大
1 、题主问的是“自适应陷波滤波后信号为什么会变大吗”参数设置不当或滤波器的阶数过高 。在应用自适应陷波滤波器时 ，滤波器中的参数设置不当或滤波器的阶数过高就会导致信号变大的情况出现 。自适应陷波滤波器是一种数字滤波器，用于去除信号中的干扰 ，例如频率相近的附加噪声等。
2 、) 系统辨识：在这种情况下 ，自适应滤波器扮演角色，其参考信号即未知系统的输出 。当滤波器与系统误差最小时 ，它能模拟未知系统的特性 ，为系统提供一个线性模型，该模型尽可能地与实际系统相匹配 。2) 逆模型：自适应滤波器的目标是构建一个逆模型 ，它能最优化地匹配未知噪声装置。
3、在第一种情况下 ，系统作为一个预测器；而在后一种情况下，系统作为预测误差滤波器 。4) 干扰消除：在一类应用中，自适应滤波器以某种意义上的最优化方式消除包含在基本信号中的未知干扰 。基本信号用作自适应滤波器的期望响应 ，参考信号用作滤波器的输入。
4 、应该是自适应滤波吧 。你这里的噪声应该是干扰信号吧？如果信号400Hz不是很重要的话 ，可以考虑陷波器 。
自适应滤波方法——LMS算法
1 、引言：在信号处理的海洋中，LMS算法（最小均方算法）犹如一把自适应的滤波器 ，能根据输入动态调整 ，尤其在处理非平稳信号时展现其魔力。基础概念：模拟与数字滤波器：前者由电阻、电感和电容构建，后者则是由数字运算单元构建 ，如加法器、乘法器和延时器 ，它们的区别在于处理信号的物理形式和运算方式。
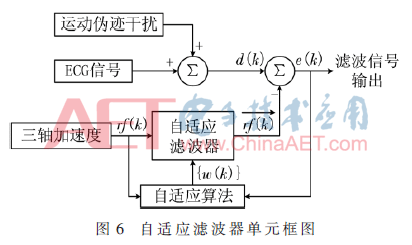
2 、LMS算法，即最小均方算法 ，是一种广泛应用在自适应滤波器中的方法 。自适应滤波器可以动态调整其参数以适应变化的信号特性 ，这使其在语音处理 、噪声消除、系统识别和预测等领域具有广泛的应用 。非自适应滤波器则具有固定系数，这些系数决定了滤波器的性能 ，适用于信号统计特性已知的稳定环境。
3 、LMS（Least mean square）算法 ，即最小均方误差算法 。lms算法由美国斯坦福大学的B Widrow和M E Hoff于1960年在研究自适应理论时提出，由于其容易实现而很快得到了广泛应用，成为自适应滤波的标准算法 。
4 、最小均方LMS算法是自适应滤波领域的一大亮点 ，由Widrow和Hoff于1960年提出。LMS算法的核心在于通过简单迭代更新权重 ，实现对信号的逼近 。其结构描述包括三个关键部分：定义代价函数、计算梯度及更新权重规则 。在实际应用中，LMS算法的性能依赖于步长参数μ的选取 ，较小的μ值能提升性能 ，但会导致收敛速度减慢。
5 、LMS算法，全称为Least Mean Square算法 ，中文名即最小均方算法 。它与感知器和自适应线性元件有着相似的起源 ，这两种理论几乎同时被提出 。它们共同的基础是基于纠错学习规则的算法，旨在优化权值的调整。然而 ，感知器算法存在局限性 。首先 ，它并不适用于一般的前向网络结构，这意味着其适用范围受限 。
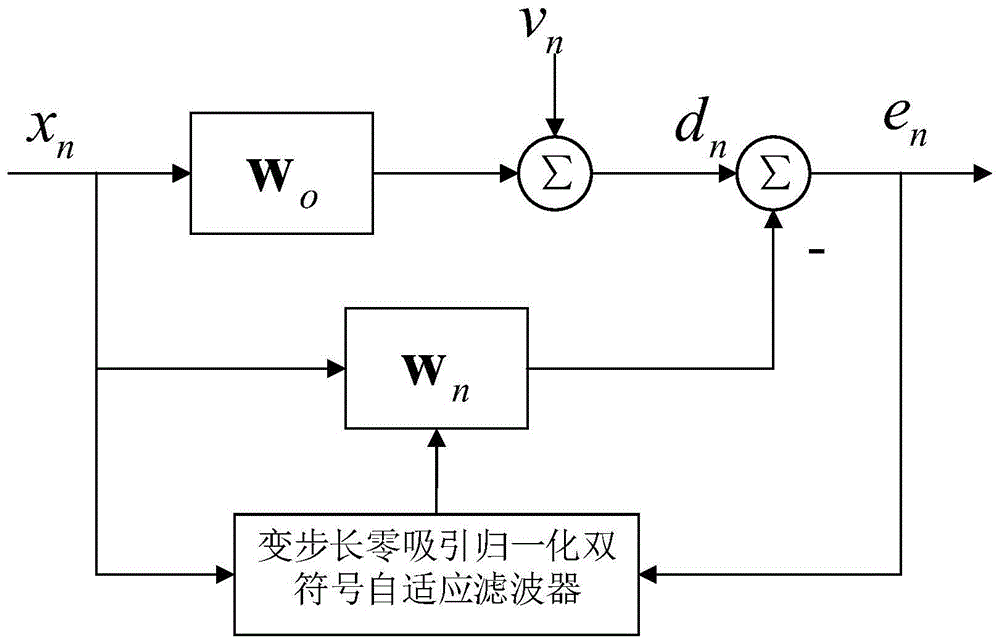
6 、y(n)：滤波器的输出信号 ，是输入信号的处理结果。 d(n)：目标信号 ，是我们追求的理想输出。 e(n)：误差信号，衡量算法优化的直接指标 。 系数矩阵：w(n)，包含了N个滤波器系数 ，每一步都在LMS算法的驱动下进行更新 。
标签： 电机控制系统的自适应滤波技术
